Deep sequence models tend to memorize geometrically; it is unclear why.

Deep sequence models tend to memorize geometrically; it is unclear why.
[Preprint: ArXiv]
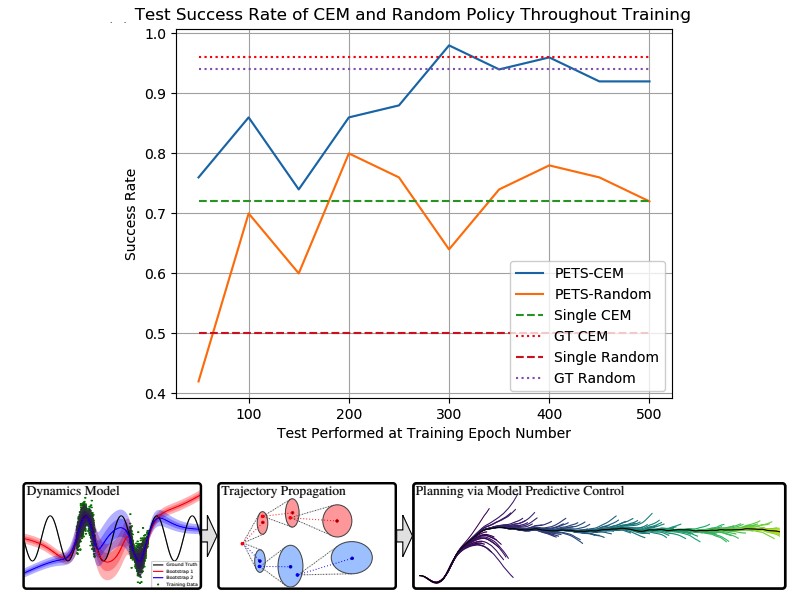
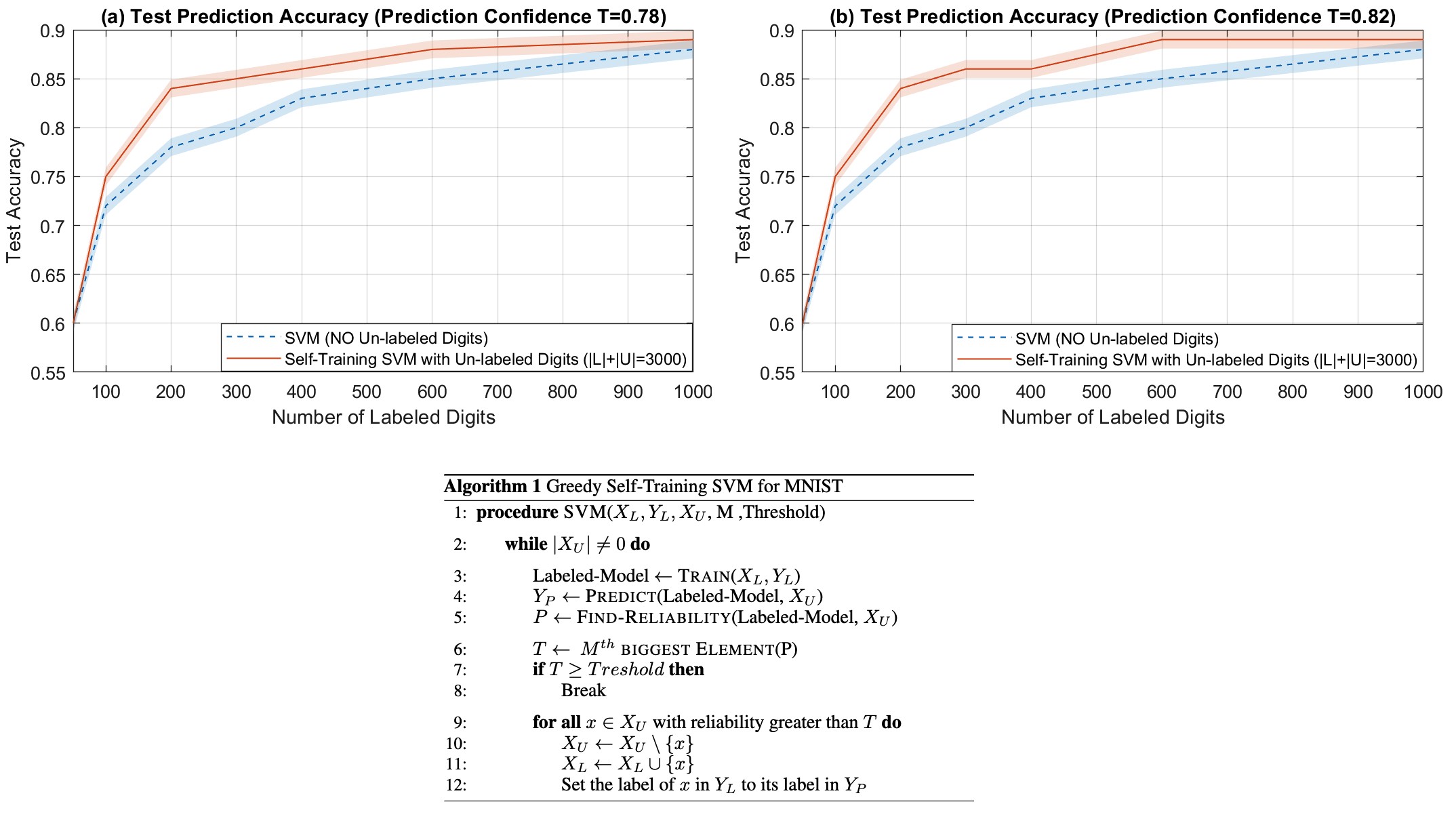
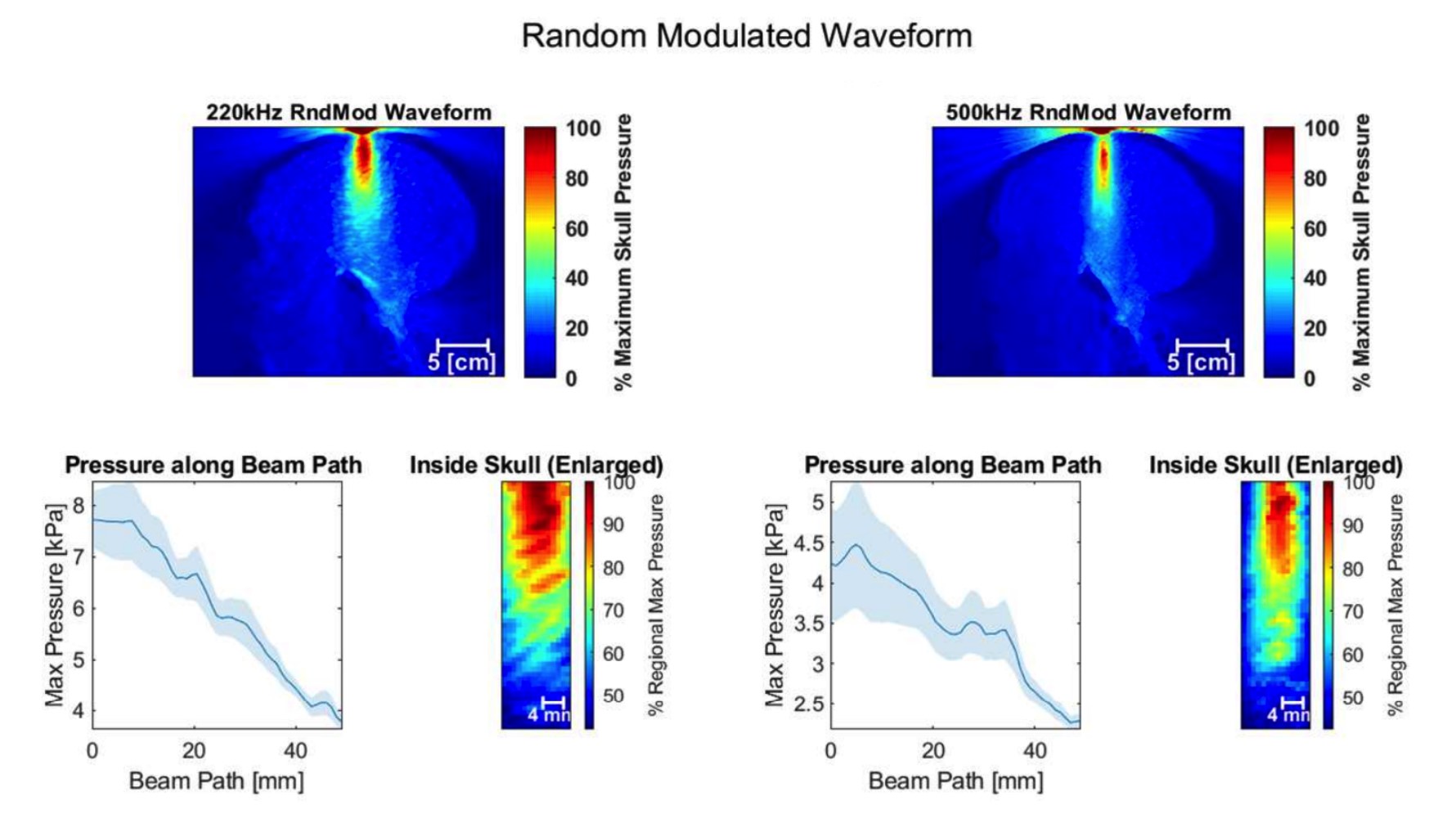
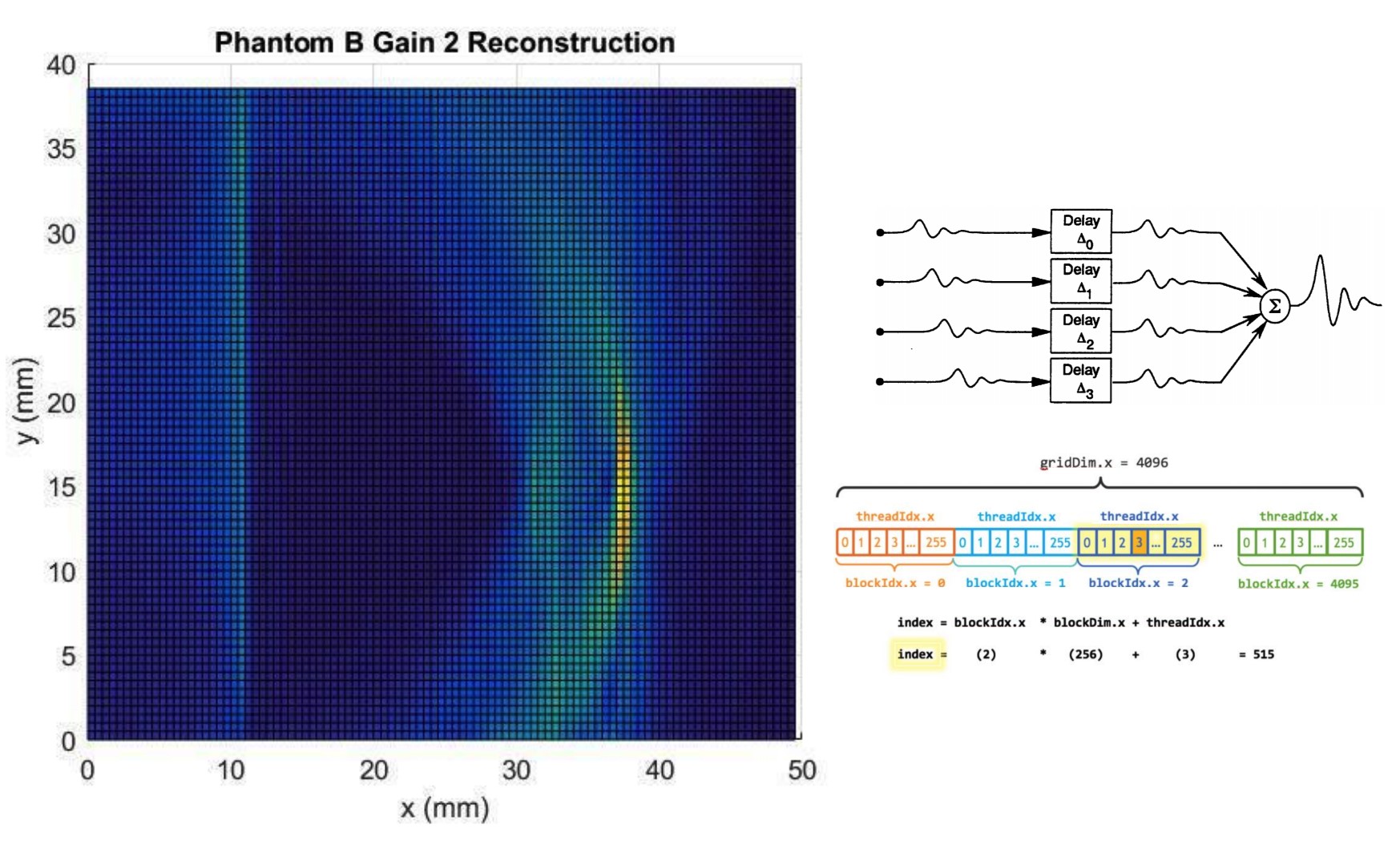
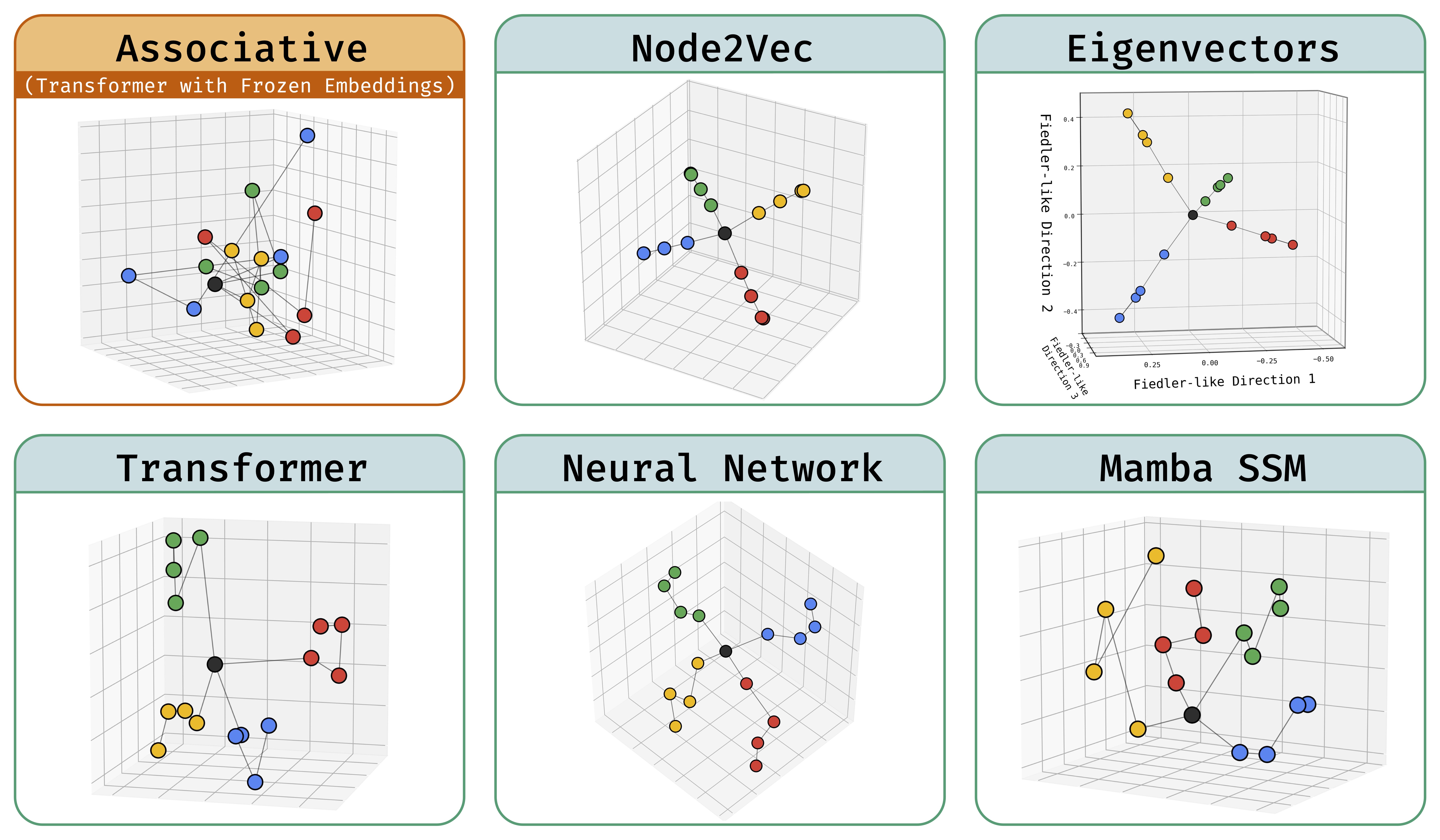
Abstract: In sequence modeling, the parametric memory of atomic facts has been predominantly abstracted as a brute-force lookup of co-occurrences between entities. We contrast this associative view against a geometric view of how memory is stored. We begin by isolating a clean and analyzable instance of Transformer reasoning that is incompatible with memory as strictly a storage of the local co-occurrences specified during training. Instead, the model must have somehow synthesized its own geometry of atomic facts, encoding global relationships between all entities, including non-co-occurring ones. This in turn has simplified a hard reasoning task involving an ℓ-fold composition into an easy-to-learn 1-step geometric task.
From this phenomenon, we extract fundamental aspects of neural embedding geometries that are hard to explain. We argue that the rise of such a geometry, despite optimizing over mere local associations, cannot be straightforwardly attributed to typical architectural or optimizational pressures. Counterintuitively, an elegant geometry is learned even when it is not more succinct than a brute-force lookup of associations.
Then, by analyzing a connection to Node2Vec, we demonstrate how the geometry stems from a spectral bias that -- in contrast to prevailing theories -- indeed arises naturally despite the lack of various pressures. This analysis also points to practitioners a visible headroom to make Transformer memory more strongly geometric. We hope the geometric view of parametric memory encourages revisiting the default intuitions that guide researchers in areas like knowledge acquisition, capacity, discovery and unlearning.